摘要 文章回顧了電子的拓撲幾何理論發展的初期,大約二十多年的曆史。首先介紹拓撲陳數在凝聚態物理中的兩個重要應用。其一關于量子霍爾效應,絕緣條件下霍爾電導可以寫成一個陳數拓撲不變量,從而解釋實驗結果的精確量子化。其二關于絕熱泵浦,它描述布洛赫能帶的絕熱電流響應,與電子極化有密切聯系。拓撲陳數是布裏淵區上貝裏曲率的積分,後者本身也有獨立的物理意義。接著介紹貝裏曲率對電子動力學的影響,包括反常速度和軌道磁化等概念。作者還將這個理論推廣到多帶情況,使其可以應用到自旋輸運等現象。最後,文中展示了再量子化方法,從半經典模型來獲得布洛赫電子的有效量子理論。在非相對論極限下,泡利—薛定谔方程可以看作是狄拉克電子在正能譜上的等效量子理論,其中的自旋軌道耦合即是一種幾何物理效應。
關鍵詞 貝裏相位,貝裏曲率,拓撲陳數,量子霍爾效應,絕熱泵浦,半經典動力學,反常速度,相空間態密度,泡利—薛定谔方程,廣義派爾斯替換
回顧了百多年來人們對固體中電子的認識曆程。從經典的自由粒子假設開始,經過量子力學的初步改造,人們有了布洛赫粒子的概念,獲得了金屬、半導體、絕緣體的基本圖像。二戰後,經過對多體相互作用的細致梳理,並發展對布洛赫能帶有效的計算方法,人們開始了基于第一性原理的對固體物理的定量研究。上世紀八十年代初,索利斯等人發現分布在布裏淵區上的布洛赫態可擁有整體的、非平庸的拓撲結構。支撐這個拓撲結構的幾何量被稱爲貝裏曲率,它刻畫了布洛赫態在動量空間裏的微分結構。本文將展開討論這些拓撲幾何概念如何進一步刷新人們對固體中電子的認識。
我們熟悉的拓撲幾何概念源于對曲面的理解。在觀察曲面時,最容易捕獲的幾何特征就是曲面在每個點處是如何彎曲的。這在數學上可用一個內禀的曲率,即高斯曲率來表征。它實際上刻畫了曲面上一個點的小鄰域與它的切平面偏差的程度。如果在這個小鄰域裏用三條短程線做一個曲面三角形,它的內角和會偏離π。偏離的程度就等于高斯曲率乘以三角形的面積。高斯曲率通過著名的高斯—博內特定理也支撐了曲面的拓撲結構:一個封閉曲面上高斯曲率的積分是個整數,可以用來刻畫曲面的拓撲,區分它是否可以連續地(不剪斷不粘連)拉扯成爲一個球面還是一個環面,或者是有多個孔的曲面。
上面說到的貝裏曲率源于1984年貝裏(Michael Berry)對于量子力學裏絕熱演化問題的思考[1]。根據量子力學中的絕熱定理,如果哈密頓量依賴一些參數,一個非簡並的能量本征態在參數緩慢變化時不會發生躍遷,只是會隨時間積累相位。積累的速率等于本征能量除以普朗克常數(也即動力學相位),再加上一個正比于參數變化率的修正。後者在參數空間裏一個閉合路徑上的積分就是貝裏相位(Box 1)。這個貝裏相位是幾何的,因爲它的表達式不依賴于參數空間內的坐標變換,就像一條曲線的長度並不依賴于曲線方程用什麽參數來表達。它還是物理的,因爲它不依賴于本征波函數的相位如何選取,具有所謂規範不變性。
BOX 1
貝裏相位
考慮一個由哈密頓量

描述的系統,其中R=(R1,R2,…)是一組隨著時間緩慢變化的外界參數。量子絕熱定理說,如果體系初始處在一個非簡並的瞬時本征態|n(R(t=0))>,以後它就會待在|n(R(t))>上,其中瞬時本征態滿足

。這個狀態的相位由含時薛定谔方程確定。除了由能量的時間積分給出的動力學相位,還有一部分可以寫爲參數空間一個線積分的幾何相位。貝裏注意到,如果系統在參數空間的演化是一個回路,這個幾何相位
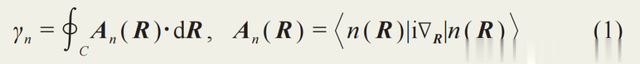
還具有規範不變性,也就是不依賴于瞬時本征態的相位如何選取,只要在參數空間裏保持單值即可。由于他的深刻見解,我們經常把幾何相位稱爲貝裏相位,把An(R)稱爲貝裏聯絡。根據斯托克斯定理,貝裏相位也可以寫爲

其中被積函數稱爲貝裏曲率。
我們考慮一個具體的例子:一個用哈密頓量

描述的兩能級系統,其中σ是泡利矩陣。它的兩個本征態的能量分別是±h。對于低能級,它的貝裏曲率是

。我們看到貝裏曲率描述了一個位于h=0的磁單極子的磁場,在h=0處兩個能級變爲簡並能級:簡並點因此表現爲貝裏曲率通量的源或漏。沿閉合路徑的貝裏相位由h在單位球上路徑的立體角的一半給出(圖1)。如果對整個球體上的貝裏曲率進行積分,我們會發現

。一般來說,貝裏曲率在閉合流形上的積分是以2π爲單位量子化,等于內部單極子的數量,這個數被稱爲陳數,因陳省身先生在微分幾何方面的工作而得名。
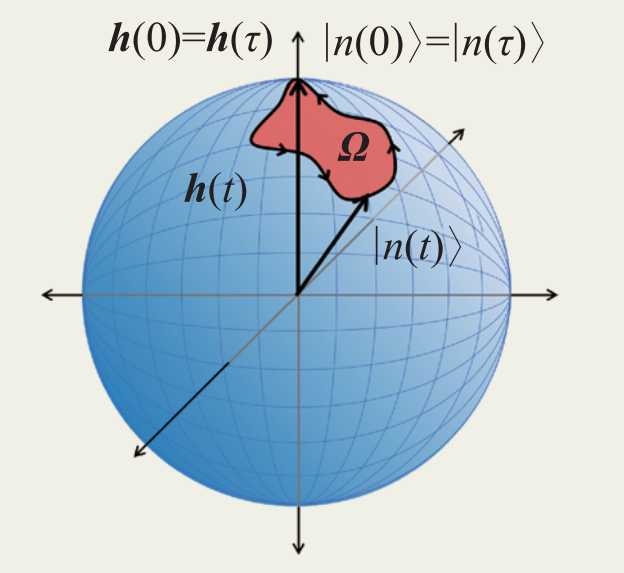
圖1 量子態的絕熱演化産生貝裏相位的示意圖
我們所說的貝裏曲率就是一個無窮小閉合路徑上的貝裏相位除以路徑所圍繞的面積,而布洛赫態所在的布裏淵區就對應于貝裏所說的參數空間。這個定義與高斯曲率有些類似,但它度量的不是參數空間本身,而是附在其上的(布洛赫)量子態隨參數變化的某種彎曲。在三維情況下,一個無窮小面積可以有不同的朝向,因此貝裏曲率就成爲布裏淵區這個動量空間上的(赝)矢量場。貝裏相位的規範不變性也傳遞到貝裏曲率上,後者在數學結構上類似于一個磁場,可以寫成動量空間上一個規範矢勢的旋度。
因此,當加州理工學院的數學物理學家Simon看到貝裏的工作時,立即聯想到索利斯等人的量子霍爾電導的表達式,評論說它其實代表了纖維叢微分幾何中的一個陳省身拓撲整數[2]。貝裏曲率在布裏淵區上的積分給出這個陳數,就如同高斯曲率的積分給出一個封閉曲面的歐拉示性數一般。早年狄拉克討論的磁單極也代表了一種拓撲陳數[3],但對其多年的物理探測一無所獲。量子霍爾效應呈現給人們的是二維布裏淵區這個環面包含的一個虛擬空間裏面的磁單極。多年以後,人們也終于在三維動量空間上找到了磁單極,就是現在固體物理學家們常說的外爾點,那裏有許多奇特的物理現象[4]。
除了拓撲陳數可以帶來令人震撼的宏觀量子化現象,貝裏曲率所代表的布洛赫態的幾何特征也不可忽視地反映在電子系統對外場的響應中,有時甚至起主導作用。前文我們曾指出,貝裏曲率出現在布洛赫電子的運動方程中。一般說來,只要體系不同時具有時間反演和空間反演對稱,或者體系的自旋軌道耦合不可忽略,貝裏曲率就非零,因而可以在更廣泛(即使陳數爲零)的條件下影響到電子的行爲。在磁單極出現的附近,貝裏曲率甚至可以發散,它引起的物理效應就尤其顯著,爲人們調制材料的性能提供了一種特殊的手段。
下面將回顧電子的拓撲幾何理論發展初期大約二十多年的曆史。主要內容將分五個小節,拓撲陳數、絕熱泵浦、運動方程、簡並情形、再量子化,對這一理論做出比前文更爲細致但仍然相對簡單的描繪[5]。其中,拓撲陳數與運動方程前文已有所提及;絕熱泵浦描述布洛赫能帶的絕熱電流響應,和電子極化密切相關。簡並情形與再量子化這兩小節將把相關幾何物理概念作適當擴展,並應用在能帶子空間內的量子化問題上。非相對論極限下的泡利—薛定谔方程就是狄拉克電子在正能譜上的等效量子理論,其中的自旋軌道耦合即是一種幾何物理效應。
01拓撲陳數
1980年,馮·克利青對半導體界面上一層二維電子氣做了低溫強磁場條件下的霍爾效應測量[6]。電子氣在厚度方向處在量子基態,因而只有平面上兩個自由度。磁場加在垂直方向,平面上一個方向通電流,另一方向測得電壓,電壓與電流的比值就是霍爾電阻(Box 2)。霍爾電阻隨磁場的變化在低場段就是一條過零點的直線,這也是前文講到的德魯德經典理論所預言,而且還可以從直線的斜率讀出電子的密度來。
BOX 2
量子霍爾效應
1980年馮·克利青發現,在強磁場下,二維電子氣的霍爾電阻以

爲單位精確量子化,同時縱向電阻消失(圖2)。嚴格的量子化是一個意外驚喜,索利斯與合作者把這個現象解釋爲電子狀態的一個拓撲特性。他們考慮了周期勢場和磁場作用下的所謂磁布洛赫能帶,發現在滿帶情況下,電場會引起一個垂直方向的電流,對應電導可以寫成

其中unk(x)是磁布洛赫函數的系數部分。從貝裏相位的角度來看,這裏的參數空間就是動量的布裏淵區,具有環面的拓撲結構(圖3)。因而,這個式子代表了一個以

爲單位的拓撲陳數,必須是量子化的。

圖2 整數量子霍爾效應(摘自Tsui D. Reviews of Modern Physics,1999,71:891)

圖3 二維布裏淵區等價于環面
但是,隨著磁場增強,直線漸漸變成從小到大的一個個台階。台階的高度可以用一個普適量子除以一個整數來表達,這個普適量子等于普朗克常數除以電子電荷的平方,大約25813 Ω。馮·克利青的實驗精度達到百萬分之一的量級,短短幾年後實驗學家們把這個精度又提高了三個數量級,超出國際上已有的實體電阻基准提供的可能衡量標准。因此,從1990年開始,國際上就改用馮·克利青發現的量子霍爾效應的平台作爲新的電阻測量基准[7]。
發生平台的地方,也伴隨著沿電流的縱向電阻的消失。前文提到,電子在強磁場下其能帶會以一條條高度簡並的朗道能級的形式呈現。而縱向電阻的消失讓人們聯想到完整的朗道能級的填充,平台所對應的那個整數就應該是有多少個朗道能級被填滿。這些填滿了的朗道能級不會在體系內部導電,但Laughlin[8]和Halperin[9]認爲電子氣的邊緣應該仍然有邊界態可以攜帶電流,但它們的流向是相反的。同向狀態的碰撞不改變電流,而反向的邊界態像高速公路那樣被隔離在兩側而互不幹擾。因此,體系不能在縱向積累電壓,但如果兩側電流有個淨差值,橫向就會有個壓降,而比例系數正是馮·克利青發現的電阻量子除以邊界態的數目。
索利斯等人按照輸運系數傳統的久保公式,考察了霍爾電導率在電子氣的內部的行爲[10]。在他們的模型裏,二維電子同時受磁場和一個周期勢的影響;之前很多人研究過,Hofstadter用數值方法還得到了能譜的細致圖像。當周期元胞裏磁通是h/e的分數時,電子本征態呈現爲類似布洛赫狀態的樣子。久保公式其實就是一個微擾論的公式,通常以速度算符在填充態和空態之間的矩陣元來表達,但索利斯等人卻把最後結果簡化成填充的布洛赫態在布裏淵區上的一個整體行爲,讓人一目了然地看到電導率必須爲e2/h的整數倍。
這一工作沒有用到朗道能級的概念,故可推廣應用到通常意義下的布洛赫能帶,比如Haldane于1988年提出的一個模型[11]。人們還發現,如果能帶的陳數非零,體系就自然會在邊界處産生單向流動的邊界態,從而攜帶量子霍爾電流[12]。2013年,薛其坤團隊首次驗證了量子化的霍爾效應可以在無磁場但有剩余磁化的條件下實現[13]。另一方面,Haldane模型被Kane和Mele應用到石墨烯[14],引發了對時間反演對稱的拓撲絕緣體的研究熱潮。
從一開始人們就在問,爲什麽實驗觀察到的量子平台可以有那麽高的精度?原子物理中的精密測量除了實驗手段的精妙,也依賴于原子系統的完全確定。固體材料和器件不可能做到完美無缺,其內部的雜質類型和分布也不完全清楚。另外,電子間也有相互作用,布洛赫態只是平均場意義下的一個單粒子近似。作者之一有幸于1982—1985年間跟隨導師索利斯,接受並解決了這一難題[15]。我們的做法是考慮多體基態波函數對周期邊界條件中相位參數的依賴,證明霍爾電導在絕緣條件下仍然可以寫成一個陳數拓撲不變量。後來,利用同樣的絕緣條件,我們又把證明中用到的周期邊條件放寬到實驗中的情形,從而徹底解決了那個精度難題[16]。
1982年,崔琦等人在高質量的二維電子器件中又發現了分數量子霍爾效應[17]。Laughlin認爲這是電子相互作用造成的特殊關聯效應,並寫出多體波函數來描述這一現象。那麽,我們的多體拓撲理論如何才能給出分數來呢?答案只能從多體基態的簡並得到,蘇武沛在周期邊界條件下的數值計算確實表明了這一點[18,19]。對此,Haldane在Aspen物理中心的一個討論會上提出了嚴重質疑,因爲他在球面上做的計算根本看不到簡並[20]。後來,在與文小剛的一篇文章裏,我們證明簡並度確實依賴于二維曲面的拓撲,才最終解決了這個爭論[21]。類似于整數情形,我們的多體拓撲理論並不依賴于強磁場的特殊條件,也可以應用到最近實驗上觀察到的分數量子反常霍爾效應[22]。
02絕熱泵浦
Laughlin在1981年論證霍爾電導量子化的時候,提出了下述的理想實驗[23]。假設可以將二維電子系統彎成一個圓柱面,然後在它的中心穿過一個緩慢增加的磁通,而原本的垂直于二維電子系統的磁場此時變爲與柱面相垂直。根據法拉第效應,變化的磁通自然會在圓周方向感應出來一個電動勢,這個電動勢在垂直柱面的外磁場下通過霍爾效應又會在柱面的縱向造成一個電流。這個霍爾電流會有多大呢?Laughlin發現,磁通增加一個量子h/e的時候,體系內部相當于做了一個規範變換,能譜和本征態都沒有發生變化;如果內部有整數個朗道能級被填充,磁通緩慢增加是個絕熱過程,不會在內部引起激發。唯一的可能只是有整數個電子在磁通增加的過程中從柱面的一端轉移到了另一端,而這個整數就是量子霍爾電導中的整數。
Laughlin關于規範不變和絕熱演化的論述可以推廣到雜質等引起的無序情形,但整數個電子轉移的推論還需要量子力學框架下的嚴格論證。1983年,索利斯考慮了在周期勢場隨時間緩慢且周期的變化時,填滿的一維布洛赫能帶絕熱演化的問題,並計算了演化過程中伴生的絕熱電流。他發現此電流可以寫成布洛赫態在時間和動量這個參數空間上貝裏曲率的積分,故一個時間周期內的電荷轉移是個陳數,必須是量子化的。這就是文獻中常提到的索利斯泵浦(Box 3)[24]。最近絕熱泵浦也在冷原子系統中被觀察到[25—27]。
BOX 3
電荷泵浦
索利斯考慮了一維絕緣體經曆循環絕熱演化的電荷泵浦問題。在這種情況下,參數空間是二維的,由晶體動量和時間t 張成,構成一個環面。索利斯發現,泵浦電荷等于Q=

,因此也是量子化的一個拓撲陳數。絕熱電荷泵浦可以作爲一個電流量子基准,它與量子霍爾效應和超導約瑟夫森效應一起,把電流I、電壓V 和頻率f 用兩個自然常數聯系了起來(圖4)。

圖4 電流—電壓—頻率的量子基准關系
如何把絕熱電荷轉移量子化的結論進一步推廣到一般情形,容許體系有雜質無序和多體相互作用呢?當時,我們還沒有想到直接攻克量子霍爾效應的一般證明。上節講到的利用周期邊條件的相位的那個方法還是首次在解決這個問題的時候找到的。我們的結論是絕緣狀態下的泵浦必然是量子化的[28]。這彌補上了Laughlin規範論說的一個邏輯漏洞,因而也可以認爲是對一般情況下量子霍爾效應的間接證明。
絕熱泵浦也提供了一個建立電流基准的途徑,因爲它的高精度由我們關于拓撲量子化的一般理論來保證,而溫度和非絕熱效應可以指數性地被抑制[29]。後來,劍橋大學的Pepper研究組利用表面聲波通過一個二維電子氣的人工結構實現了這一設想[30]。他們觀察到一系列電流的平台,等于整數個電子電荷與頻率的乘積,實驗精度達到20個ppm(百萬分之一,精密測量領域常用的標示)。這些平台對應于每個勢阱有整數個電子占據,其中包括奇數。理論分析表明,電子的庫侖相互作用非常重要,確實需要一個多體拓撲理論來保證絕熱泵浦的精度。
最新的這類實驗已經把精度提高到了0.1 ppm的水平[31],再提高一個數量級就可以實現量子化的電流基准,取代傳統上基于導線之間安培力的測量。上節我們講到,量子霍爾效應已經于1990年在國際上被采用爲新的電阻基准。同時被采用的還有一個基于超導約瑟夫森效應的電壓基准,它把電壓降表達爲頻率乘以超導磁通量子(h/2e)[32]。如果能補充上基于量子電荷泵浦的電流基准,人們就有了完整的基于電子電荷、普朗克常數和頻率的三個基本的量子電測量手段。這裏,頻率的測量最終基于原子鍾,其原理也是一個量子現象。
順著索利斯絕熱泵浦的思路,我們也可以得出一個電荷密度量子化響應的結論[33]。比如,如果一個周期勢場裏的電子體系處在絕緣狀態,電荷密度就是某個整數除以元胞的大小,其中奇數對應于莫特絕緣體情形。如果有多個非公度周期場,絕緣態中電子的密度就等于這樣一些項的加和,其中每項都是某個整數除以一種元胞的大小。在一維情況下,索利斯就得到過這個結論。在二維情況下,如果電子還受到磁場的影響,絕緣狀態下的密度還要加上正比于磁場和霍爾電導的一項,正如早先瓦尼爾給出的結論一樣[34]。
絕熱電流的概念也可以用到絕緣體中電極化強度的計算。在布洛赫波的觀念下,晶體中的電子不能被認爲是束縛在任何一個特定的原子上,因而基于電偶極子概念的計算都不成立。King-Smith和Vanderbilt注意到,如果通過選擇相位規範使得布洛赫態在布裏淵區上具有周期性,索利斯關于絕熱電流的表達式就可以寫成一個Zak相位(布洛赫態沿著布裏淵區一大圈的貝裏相位[35])對時間的導數。這導致了那個著名的用Zak相位來表達電極化強度的式子,大大方便了後者的第一性原理計算[36]。需要考慮多體效應的時候,也可以利用多體基態波函數對于周期邊條件的相位依賴而把這個Zak相位的概念加以推廣[37]。
03運動方程
前面講到,索利斯等人發現的拓撲陳數是布裏淵區上貝裏曲率的積分,那麽後者是否還有獨立的物理意義呢?爲了理解Hofstadter能譜的分形結構[38],在單元格包含的磁通爲有理數倍磁通量子的情況下,我們仔細研究了布洛赫能帶中波包的運動規律(Box 4)[39]。我們發現,除了通常由能譜給出的群速度之外,電子的速度還有個正比且垂直于外力的反常項,其比例系數就是布洛赫態的貝裏曲率。在零磁場情況下,這個反常速度早年曾被Karplus和拉廷格發現並用來解釋反常霍爾效應,但可惜沒有引起持續的重視[40]。
BOX 4
波包動力學
貝裏曲率本身也可以參與布洛赫電子的波包動力學。我們發現,在外部電磁場存在的情況下,波包的運動方程由下式給出:

其中

這一項被稱爲反常速度,它是磁性金屬中反常霍爾效應的來源。如果系統具有時間反演對稱性,則有Ωn(k)=-Ωn(-k);如果系統具有空間反演對稱性,則有Ωn(k)=Ωn(-k)。因此,對于同時具有時間反演對稱性和空間反演對稱性的材料,貝裏曲率消失(如果考慮電子自旋,還要對自旋指標求迹)。下圖分別反映了單晶鐵(時間反演破缺,圖5(a))和單層MoS2(空間反演破缺,圖5(b))的動量空間中貝裏曲率的分布。
除了反常速度,能量也被軌道磁矩mn(k)所修正,

。軌道磁矩來源于波包的自轉,與g因子密切相關。
波包動力學的另一個關鍵因素是相空間的體積測度不再是一個常數。這是因爲在貝裏曲率和磁場存在的情況下,波包的動量和位置不再是一對正則坐標。通過研究相空間中體積元隨時間的演化,我們發現態密度被修正爲

才能保證相空間量子狀態的數目在演化中守恒。
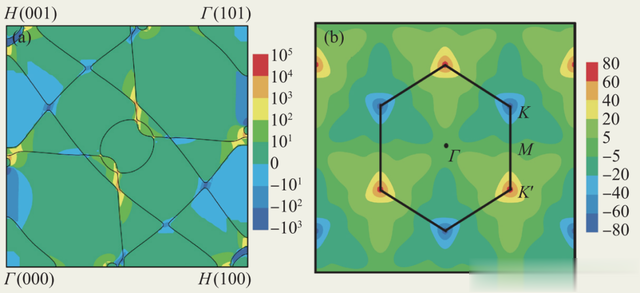
圖5 單晶鐵(a)和單層MoS2(b)的貝裏曲率在動量空間中的分布(分別摘自文獻[47]和Feng W et al. Physical Review B,2012,86:165108)
圖5單晶鐵(a)和單層MoS2(b)的貝裏曲率在動量空間中的分布(分別摘自文獻[47]和FengWetal.PhysicalReviewB,2012,86:165108)
我們還發現,一般情況下,波包除了平動以外還會有自轉,這會讓電子獲得一個磁矩,被稱爲軌道磁矩。這個磁矩在外磁場中讓能量發生塞曼移動,其動量依賴也會影響到電子的平動群速度。對于真空中自由電子在狄拉克能帶裏的波包,也有這種自轉引起的磁矩,正好對應自旋的玻爾磁子[41]。固體物理中,人們習慣用非相對論極限下的泡利—薛定谔方程來描述電子的量子行爲,自旋塞曼項被單獨列出。
運動方程的推導利用了變分方法,在計算波包的拉格朗日量的時候使用了局域和絕熱近似,因爲直接進入薛定谔方程的是規範勢,其在弱外場情況下可以寫成隨時空緩慢變化的函數。1999年Sundaram利用了同樣的技術,考慮到更一般的緩變微擾,推導出來的運動方程涉及到相空間和時間域裏方方面面的貝裏曲率分量[42]。這個方程後來有更廣闊的應用,但本文不打算展開討論,我們把目光仍然聚焦在電磁場作用的情形。
動量空間貝裏曲率在學界受到廣泛的重視,還是得益于在反常霍爾效應中的成功應用。2002年在與Jungwirth 和 MacDonald合作的一個工作中,我們具體研究了一個鐵磁半導體材料中的貝裏曲率,計算了反常速度引起的霍爾電導,發現與實驗結果相當符合[43]。以前近半個世紀,人們習慣了用Smit的偏斜散射[44]或者Berger的散射橫移[45]等外禀機制去理解反常霍爾效應,缺乏定量的理論檢驗。我們這項工作重新確立了早年由Karplus和拉廷格首次提出的內禀機制,開啓了這個領域的定量研究[46]。
由于貝裏曲率完全由布洛赫態決定,單晶體材料的這種內禀反常霍爾效應完全可以納入第一性原理計算。比如,姚裕貴等人研究了體心立方結構的鐵單晶材料[47],方忠等人也考慮了金屬鐵磁體SrRuO3[48],獲得貝裏曲率在布裏淵區的詳細分布。由此積分獲得的反常霍爾電導與實驗結果也有很好的對應。由于自旋軌道耦合所造成的能帶精細結構,貝裏曲率的分布在好幾個數量級上正負波動,曾令人十分擔心計算結果的精確程度。但是,後來王新傑等人用另一種方法,利用瓦尼爾函數插值,完全重複了姚裕貴等人的計算結果[49]。
除了反常速度,貝裏曲率還會引起態密度的改變[50]。在經典統計力學中,微觀狀態的數目是以相空間的體積來度量的,度量的單位在半經典極限下被確定爲普朗克常數的d 次方,其中d 是體系的空間維度。2005年,肖笛等人發現,受貝裏曲率的影響,相空間的體積元會隨時間演化而改變。爲了維持體積元中的狀態數目不變,量子態密度就要有個正比于貝裏曲率和磁場的修正。這樣,許許多多宏觀物理性質就可以通過貝裏曲率被磁場所調控。
作爲一個典型案例,電子的自由能就有這麽一個修正,其對磁場的微商給出電子系統的一個反常的磁化強度。磁化強度的正常項來自于電子能量對磁場的依賴,等于電子磁矩的加和平均。這個反常磁化強度蘊藏豐富的物理,當化學勢或者溫度有個空間梯度造成的統計力,它會導致一個反常霍爾和能斯特電流[51]。類似地,在體系的邊緣處由于約束電子的勢場具有非均勻性,它也會導致一個宏觀的霍爾環流。
04簡並情形
貝裏于1984年得出的幾何相位與曲率,適用于非簡並量子態的絕熱演化。同一年,維爾切克(Frank Wilczek)與徐一鴻將幾何相位的理論推廣至簡並量子態[52],幾何相位成爲簡並空間裏的一個幺正變換,而貝裏聯絡和貝裏曲率成爲矩陣。一般說來,晶體若同時具有時間和空間反演對稱,自旋相關的兩條能帶在動量空間將處處重合。人們也研究過四重簡並能帶,探討其中的高階拓撲特性[53]和自旋霍爾效應[54]。
簡並能帶中波包的運動方程該怎麽寫呢(Box 5)?2005年Culcer等人以及Shindou等人分別對此做了推廣,發現除了貝裏曲率、自轉角動量等須改爲矩陣之外,波包運動方程的形式與非簡並時大致相同。除此之外,還應附加一個旋量方程描述簡並能級裏的內在自由度的變動[55,56]。當內在自由度爲自旋時,這套方程即可來研究固體中的自旋輸運現象。
BOX 5
簡並能態的半經典動力學
簡並能態裏的波包,除了位置r與動量ħk之外,還帶有赝自旋變量ηa(a=1,2,…,N),描述波包在各能帶的占比。其運動方程式爲

其中我們用到了愛因斯坦求和規則。除此之外,貝裏聯絡R 和貝裏曲率Ω 皆成爲N 階矩陣,

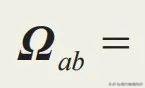

。波包中心的運動方程稍有變化,
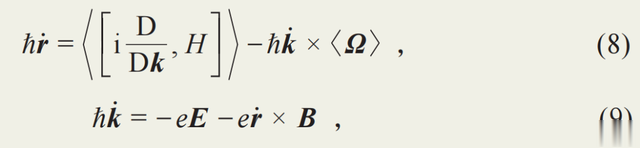
其中D/Dk爲協變導數,其形式類似D/Dt,只是t 置換爲k,而

爲赝自旋平均。
這套理論不只適用于固體能帶,也適用于狄拉克的相對論性電子理論。這時電子的能帶有正、負兩支,每支均爲雙重簡並。我們發現在正能帶低(非相對論電子),

,其中λc=h/mc爲康普頓波長,σ爲泡利矩陣。另外,計算表明,波包自轉的軌道角動量爲L=ℏσ,是自旋角動量的兩倍,解釋了爲何自旋的磁矩會帶有一個ge=2的因子。
探討波包運動軌迹時,需要知道能帶的貝裏曲率與自轉角動量。對于簡並能級,自旋方程裏除了塞曼能還有一個貝裏矢量勢,反映了軌道運動對自旋的一種非阿貝爾幾何物理效應。除此之外,波包自轉所造成的磁矩,正是能帶裏電子或空穴的反常磁矩,這會讓自旋的g因子值偏離于2。
以石墨烯模型爲例,當空間反演對稱被破壞時,狄拉克點處會出現能隙,使得載流子的貝裏曲率與自轉磁矩皆不爲零,在兩個狄拉克谷間大小相等符號相反。所以施加電場後,這兩類谷載流子會往相反的橫向移動,造成谷霍爾效應[57],表現爲樣品兩側反方向的磁化[58]。
在真空中電子的狄拉克相對論性量子理論裏,有正、負兩個能譜分支以巨大的能隙相隔,各自具有二重簡並。非相對論電子的等效理論基于正能量分支底部的性質。有意思的是,即便在真空裏存在時間和空間反演對稱,電子波包的貝裏曲率並非爲零,而是正比于自旋[59]。在外加電場下,貝裏曲率給出垂直于電場和自旋的橫向位移,反映了電子的自旋軌道耦合。黃克孫也曾于1952年提過類似的圖像,相對論性電子的顫動現象可以想像爲是平移與自轉疊加後的結果[60]。
量子力學發展初期,人們曾試圖以自轉的電荷球解釋電子自旋。如果把電荷球的庫侖勢能理解爲電子質量的相對論來源,人們就會得到一個所謂的電子經典半徑,大約等于玻爾半徑乘以精細結構常數的平方。但是,爲了得出自旋的角動量和玻爾磁子,轉動的電荷球在表面的速率須大大超過光速,此圖像因而被舍棄。
其實,非相對論電子應該被理解爲正能帶底部的一個波包。由于量子度規的限制,電子波包的尺度不能小于康普頓波長,這較經典電子半徑大了兩個數量級,沒有上述的問題。的確,波包自轉軌道角動量等于自旋角動量的兩倍,也給出一個玻爾磁子,解釋了自旋的g因子爲什麽是2。因此,用電子波包來理解,早年的自轉電荷球圖像就對了。
05再量子化
完美晶體的能帶結構,會因爲受到雜質、外加磁場、邊界等影響而變動。探討其能譜時,通常並非重頭求解薛定谔方程。較簡單的做法是以能帶爲基礎,將理論再次量子化。例如,爲了計算能帶因外加磁場所造成的分裂,昂薩格提出類似玻爾—索末菲量子化的量子化條件,由布裏淵區裏回旋軌道面積的量子化得出朗道能級,並用來解釋德哈斯—範阿爾芬效應,推斷費米面的形狀[61]。
Kuratsuji等人發現,當體系存在貝裏曲率時,玻爾—索末菲的作用量積分需因閉合的積分軌迹上積累的貝裏相而做修正[62]。之後在固體的波包理論裏也發現了類似的修正項,這個修正會影響朗道能級的位置。例如石墨烯中的狄拉克點是貝裏曲率的奇點,故動量空間中電子軌迹環繞狄拉克點一圈後的貝裏相位爲π。這會造成所有朗道能級移動半階,從而可在位于能量零點的狄拉克點處出現。
不可積體系由于經典軌道不封閉,不適用于玻爾—索末菲的量子化方法。更爲一般的做法是正則量子化,也就是將物理量轉變爲算符。例如半導體裏摻入一個受主原子,在計算其能級時並非以“晶體加雜質”的總勢能重新求解,而是由已知能帶出發,先將布洛赫電子近似爲有等效質量的自由電子,這時已不再需要考慮晶格,然後將其動量轉化爲算符。考慮受主的電勢能後得出類氫原子模型,而雜質能級即爲類氫原子能級。
計算能帶因外加磁場而分裂爲朗道能級時,若采用正則量子化,則是以派爾斯替換將能帶中的波矢轉變爲梯度算符加磁矢勢。如此一來,布洛赫能帶函數即成爲再量子化理論中的哈密頓量,求解其薛定谔方程之後即得到Hofstadter量子能譜。這種再量子化方法的嚴謹性,約于1950年由斯萊特、拉廷格等人加以確認[63,64],但他們的推導用到了局域的瓦尼爾函數,只適用于陳數爲零的能帶。
具有貝裏曲率的半經典力學,其豐富的規範結構成了再次量子化的障礙。關鍵還是在于找出正則變量,而達布定理可確保正則變量在相空間局部的存在。微擾計算表明,波包動量與正則動量的主要差異仍然是磁矢勢,而波包位置與正則位置的主要差異是貝裏聯絡,另加電磁場的一階或高階項。這種廣義派爾斯替換體現了相空間中更爲豐富的規範結構,是正則量子化方法的關鍵步驟[59]。
以狄拉克的相對論性電子理論爲例,其正能譜子空間裏的等效理論是二分量的泡利理論。傳統上這是以Foldy—Wouthuysen變換得出,也就是經由幺正變換將狄拉克哈密頓矩陣塊對角化,移除矩陣裏因外場導致的電子、空穴耦合項,得出適用于正能譜子空間的等效理論[65]。科恩曾于1959年以類似的方法得出單一能帶的等效理論[66]。由于涉及的能帶數目衆多,這是項令人生畏的艱巨推導。這個工作後來曾由Roth、Blount等人加以簡化[67,68]。
從半經典波包理論出發更容易得出等效量子理論,也有更清晰的物理圖像。我們先得到狄拉克正能譜的波包能量,然後以廣義派爾斯替換將能量函數再量子化,其結果正是泡利理論的等效哈密頓量。其中有個自旋軌道耦合項,來源于電勢能中正則位置和波包位置的差異,即非阿貝爾貝裏矢量勢。
06總結和展望
通常我們考察一個量子體系對外界的響應時,微擾論的結果往往以填充態和空態之間的矩陣元來表達外場的作用。索利斯等人在研究量子霍爾效應時發現,霍爾電導可以表達成爲填充態在動量空間的一個微分形式的積分,把霍爾電導的精確量子化解釋成爲了填充態的拓撲不變量陳數。索利斯關于絕熱泵浦的量子化結論也是表達成爲了填充態在參量空間(動量和時間)的這種幾何拓撲特征。
這個後來被稱爲貝裏曲率的微分形式強調的是填充態之間的橫向聯系,而不是與空態之間的縱向關系。在黎曼幾何中,高斯曲率強調的也是曲面的內禀性質,盡管它也可以更直觀地從包含曲面的一個高維平直視角來表達。一般情況下,我們用的量子力學模型的態空間在整體上往往是幾何平直的,因而也是拓撲平庸的。非平庸的拓撲只是發生在狀態的子空間上,比如一個或幾個能帶。
代表這個子空間橫向聯系的貝裏曲率會影響布洛赫粒子在能帶中的運動,應該是一件恰如其分的事情。如果說布洛赫當年發現了電子的動量空間被限制到了一個有限而周期的區域,半個多世紀以後的80年代以來,我們才真正認識到了這個區域上的拓撲與內禀幾何。粒子運動不但受到周期能動量關系的直接影響,也受到貝裏曲率引起的非正則相空間結構的制約。這個非正則結構也改變了能帶子空間上的統計測度和有效量子理論。
上世紀50年代,很多物理學前輩曾經努力構造單帶、雙帶等子空間上的有效量子理論。由于量子理論是用正則變量來表達的,而有效哈密頓量往往只適用于能帶的某個局部,我們所講的拓撲和幾何是顯示不出來的。能夠顯示的應該是物理位置和動量與相應正則變量之間的關系,也就是新的派爾斯替換,其中出現了磁矢勢和貝裏聯絡。如果能帶的拓撲非平庸,貝裏聯絡只能分片定義,正則變量以及相應的量子理論也只能分片成立。
時間反演破缺是反常霍爾效應出現的必要條件。早期研究的實際體系絕大多數是鐵磁體,但後來發現反鐵磁也可以承載這種效應,只要某些空間對稱也被破缺。我們完全有理由期待,將來會有陳數非零甚至分數量子化的非鐵磁絕緣材料被發現。在時間反演對稱的體系裏,貝裏曲率仍然可以非零,只要有自旋軌道耦合存在或者空間反演破缺。這可導致自旋/谷霍爾效應。
量子自旋霍爾效應在自旋不守恒的情況下仍然可以保持一種微妙的二重拓撲特征,而且也有邊界態的對應,但能帶內部似乎找不到支撐這種拓撲的幾何特征。這有點像具有空間反演對稱的絕緣晶體,其中電極化強度可以爲零(整格矢)也可以不爲零(半整格矢),但相應Zak相位的積分表達式的被積函數是個規範依賴的量,因而在局部沒有確定的物理意義。
貝裏曲率的應用遠遠不止反常霍爾效應和本文提到的軌道磁化。後續我們將系統介紹這些幾何拓撲概念在各種響應問題中的應用。除了電磁場,我們還將涉及其他物理量(比如溫度、應變和序參量)的梯度場。除了電流和熱流,我們也會考慮非守恒物理量(比如自旋)的産生與輸運。在這些線性交叉和非線性響應中,相空間的各種貝裏曲率及其高階形式以及新的幾何量(比如量子度規和位移)也會出現。
作者:牛謙 張明哲 肖笛
(1 中國科學技術大學物理學院)
(2 台灣師範大學物理系)
(3 華盛頓大學物理系和材料系)
